Goldbarts Schatztal: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 5: | Zeile 5: | ||
== [[Datei:Icon_gluehbirne.png|20px|Icon]] Aufgabenstellung == | == [[Datei:Icon_gluehbirne.png|20px|Icon]] Aufgabenstellung == | ||
Der micro:bit soll einen zufällig erstellten Weg durch das Schatztal auf seiner LED-Matrix anzeigen. | Der micro:bit soll einen zufällig erstellten Weg durch das Schatztal auf seiner LED-Matrix (Leuchtdioden-Matrix) anzeigen. | ||
Das Schatztal ist ein Raster auf dem Boden aus 5 x 5 Feldern. Die Felder sind klar erkennbar und die Schülerinnen und Schüler können bequem darauf stehen (ca. 20 x 20cm). Die Felder sind entweder geeignet große Bodenfliesen oder mittels Straßenkreide oder Klebeband am Boden markiert. | Das Schatztal ist ein Raster auf dem Boden aus 5 x 5 Feldern. Die Felder sind klar erkennbar und die Schülerinnen und Schüler können bequem darauf stehen (ca. 20 x 20cm). Die Felder sind entweder geeignet große Bodenfliesen oder mittels Straßenkreide oder Klebeband am Boden markiert. | ||
<gallery mode="packed-hover" heights=300px}> | <gallery mode="packed-hover" heights=300px}> | ||
Image:GbSt Bodenraster 201819.JPG|aufgeklebtes Raster | Image:GbSt Bodenraster 201819.JPG|Am Boden aufgeklebtes Raster | ||
Image:GbSt Bodenquadrat 201819.JPG| | Image:GbSt Bodenquadrat 201819.JPG|5 x 5 geeignet große Bodenfliesen mit Klebeband umklebt | ||
</gallery> | </gallery> | ||
Kapitän Goldbart durchquerte vor vielen Jahren dieses Schatztal. Auf seiner Reise vergrub er jeden Abend einen Schatz. Fünf Schätze sind insgesamt im Schatztal versteckt. Das Ziel der Schatzsucher ist es den Weg von Kapitän Goldbart wiederzufinden und alle | Kapitän Goldbart durchquerte vor vielen Jahren dieses Schatztal. Auf seiner Reise vergrub er jeden Abend einen Schatz. Fünf Schätze sind insgesamt im Schatztal versteckt. Das Ziel der Schatzsucher ist es den Weg von Kapitän Goldbart wiederzufinden und alle fünf Schätze zu heben. | ||
Ungefähr | Ungefähr sieben Schülerinnen und Schüler gehen gemeinsam auf Schatzsuche. Eine Schulklasse teilt sich somit in drei Gruppen Schatzsucher und drei Spielleiter auf. Jede Gruppe Schatzsucher sucht in ihrem eigenen Schatztal. Die Gruppe Schatzsucher beginnt an einer Seite des Schatztals, der Spielleiter an der rechts angrenzenden Seite. | ||
Der Spielleiter hat den micro:bit in der Hand. Wenn er auf die Taste A drückt zeigt ihm dieser, auf welchem Weg durch das Schatztal die Schätze vergraben sind. Der Weg geht von links nach rechts auf der micro:bit LED-Matrix. | |||
Diese befinden sich auf Goldbarts Route durch das Tal. | <gallery mode="packed-hover" heights=300px}> | ||
Image:GbSt_Pfadraster1.png|Weg1 in Raster | |||
Image:GbSt Pfadrastermicrobit1.png|Weg1 auf der LED_Matrix | |||
</gallery> | |||
<gallery mode="packed-hover" heights=300px}> | |||
Image:GbSt_Pfadraster2.png|Weg2 in Raster | |||
Image:GbSt Pfadrastermicrobit2.png|Weg2 auf der LED-Matrix | |||
</gallery> | |||
Jede LED entspricht also einem Feld auf dem Schatztal: | |||
<gallery mode="packed-hover" heights=300px}> | |||
Image:Microbit raster Gif.gif|Raster und micro:bit | |||
</gallery> | |||
Der erste Schatzsucher betritt nun das Schatztal. Der Spielleiter vergleicht mit dem micro:bit ob auf dem Feld ein Schatz liegt. Die Gruppe Schatzsucher gräbt nach dem Schatz mit 20 Kniebeugen. | |||
Diese befinden sich auf Goldbarts Route durch das Tal. Der Spielleiter kennt Goldbarts Route, die Schatzsucher nicht. | |||
Einer der Schatzsucher betritt nun das Spielfeld. Nun müssen alle Schatzsucher nach dem Schatz graben auf diesem Feld, dazu müssen Sie 20 Kniebeugen (oder eine andere Übung) in der Gruppe aufteilen und machen. Der Schatzsucher auf dem Spielfeld geht nun weiter geradeaus oder diagonal und die Schatzsuchergruppe muss wieder nach dem Schatz graben. Wenn der Schatzsucher durch alle Felder gegangen ist, dann sagt die Spielleitung, wie viele Schätze auf der Route waren. Der Schatzsucher geht zurück zu seiner Gruppe und ein anderer Schatzsucher beginnt seinen Weg durch das Tal. Das Ziel des Spiels ist es, das die Schatzsuchergruppe genau auf Goldbarts Route geht und alle 5 Schätze hebt. | |||
Dazu müssen die Schatzsucher in der Gruppe gut zusammenarbeiten und ihre jeweiligen Stärken finden. Einige von ihnen müssen sich bereits gegangene Wege merken und nachdenken welche neuen Wege die Gruppe ausprobieren soll. Einige müssen mehr graben für die Gruppe. | Dazu müssen die Schatzsucher in der Gruppe gut zusammenarbeiten und ihre jeweiligen Stärken finden. Einige von ihnen müssen sich bereits gegangene Wege merken und nachdenken welche neuen Wege die Gruppe ausprobieren soll. Einige müssen mehr graben für die Gruppe. | ||
| Zeile 35: | Zeile 55: | ||
Für das Spiel Goldbarts Schatztal muss sich der Spieleleiter Goldbarts Route durch das Tal überlegen. Kannst du ein Programm schreiben, damit dein micro:bit sich sofort einen zufälligen Weg durch das Tal überlegt, damit keine Pause zwischen den Spielen sein muss? | Für das Spiel Goldbarts Schatztal muss sich der Spieleleiter Goldbarts Route durch das Tal überlegen. Kannst du ein Programm schreiben, damit dein micro:bit sich sofort einen zufälligen Weg durch das Tal überlegt, damit keine Pause zwischen den Spielen sein muss? | ||
| Zeile 135: | Zeile 141: | ||
</li><li> Vereinfachung: nur ein zufälliges Feld pro Spalte programmieren, statt einem zusammenhängenden Pfad | </li><li> Vereinfachung: nur ein zufälliges Feld pro Spalte programmieren, statt einem zusammenhängenden Pfad | ||
</li><li> Es sollen auch Pfade möglich sein, die nach unten, nach oben oder zurück gehen. | </li><li> Es sollen auch Pfade möglich sein, die nach unten, nach oben oder zurück gehen. | ||
</li><li> Baue einen Zähler ein, der mit der Taste B die gefundenen Schätze mitzählt und mit Schütteln diese 2 Sekunden lang anzeigt. | |||
</li><li> Mit dem vorliegenden Lösungsprogramm ist es ein wenig wahrscheinlicher, wenn die LED in der vorigen Spalte am Rand leuchtet, dass auch die LED in der nächsten Spalte am Rand leuchtet. Kannst du das Programm umschreiben, so dass es gleich wahrscheinlich ist, dass die LED am Rand oder ein Feld weiter drinnen leuchtet? | </li><li> Mit dem vorliegenden Lösungsprogramm ist es ein wenig wahrscheinlicher, wenn die LED in der vorigen Spalte am Rand leuchtet, dass auch die LED in der nächsten Spalte am Rand leuchtet. Kannst du das Programm umschreiben, so dass es gleich wahrscheinlich ist, dass die LED am Rand oder ein Feld weiter drinnen leuchtet? | ||
</li></ol> | </li></ol> | ||
Version vom 8. Oktober 2019, 13:24 Uhr
Für scharfe Denker
Die 3A Klasse spielt in Turnen das Spiel Goldbarts Schatztal. Die Schatzsucher müssen dabei Schätze im Schatztal suchen. Der Spielleiter überprüft wie viele Schätze gefunden wurden. Maria ist gerade Schatzsucherin und Lukas ist Spielleiter. Maria kommt aus dem Schatztal. Du hast keinen Schatz gefunden, sagt Lukas zu ihr. Du schummelst doch, schreit Maria. Wir brauchen jemand Unparteiischen, der vorgibt wo die Schätze liegen. Der micro:bit kann das, meint Alexandra.
 Aufgabenstellung
Aufgabenstellung
Der micro:bit soll einen zufällig erstellten Weg durch das Schatztal auf seiner LED-Matrix (Leuchtdioden-Matrix) anzeigen.
Das Schatztal ist ein Raster auf dem Boden aus 5 x 5 Feldern. Die Felder sind klar erkennbar und die Schülerinnen und Schüler können bequem darauf stehen (ca. 20 x 20cm). Die Felder sind entweder geeignet große Bodenfliesen oder mittels Straßenkreide oder Klebeband am Boden markiert.
-
Am Boden aufgeklebtes Raster
-
5 x 5 geeignet große Bodenfliesen mit Klebeband umklebt
Kapitän Goldbart durchquerte vor vielen Jahren dieses Schatztal. Auf seiner Reise vergrub er jeden Abend einen Schatz. Fünf Schätze sind insgesamt im Schatztal versteckt. Das Ziel der Schatzsucher ist es den Weg von Kapitän Goldbart wiederzufinden und alle fünf Schätze zu heben.
Ungefähr sieben Schülerinnen und Schüler gehen gemeinsam auf Schatzsuche. Eine Schulklasse teilt sich somit in drei Gruppen Schatzsucher und drei Spielleiter auf. Jede Gruppe Schatzsucher sucht in ihrem eigenen Schatztal. Die Gruppe Schatzsucher beginnt an einer Seite des Schatztals, der Spielleiter an der rechts angrenzenden Seite.
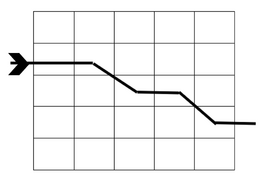
Der Spielleiter hat den micro:bit in der Hand. Wenn er auf die Taste A drückt zeigt ihm dieser, auf welchem Weg durch das Schatztal die Schätze vergraben sind. Der Weg geht von links nach rechts auf der micro:bit LED-Matrix.
-
Weg1 in Raster
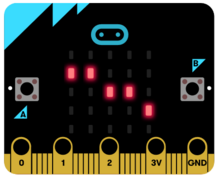
-
Weg1 auf der LED_Matrix
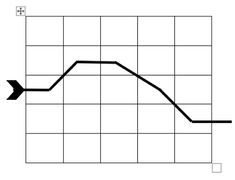
-
Weg2 in Raster
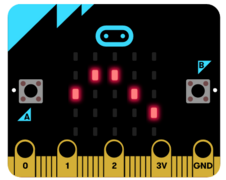
-
Weg2 auf der LED-Matrix
Jede LED entspricht also einem Feld auf dem Schatztal:
-
Raster und micro:bit
Der erste Schatzsucher betritt nun das Schatztal. Der Spielleiter vergleicht mit dem micro:bit ob auf dem Feld ein Schatz liegt. Die Gruppe Schatzsucher gräbt nach dem Schatz mit 20 Kniebeugen.
Diese befinden sich auf Goldbarts Route durch das Tal. Der Spielleiter kennt Goldbarts Route, die Schatzsucher nicht.
Einer der Schatzsucher betritt nun das Spielfeld. Nun müssen alle Schatzsucher nach dem Schatz graben auf diesem Feld, dazu müssen Sie 20 Kniebeugen (oder eine andere Übung) in der Gruppe aufteilen und machen. Der Schatzsucher auf dem Spielfeld geht nun weiter geradeaus oder diagonal und die Schatzsuchergruppe muss wieder nach dem Schatz graben. Wenn der Schatzsucher durch alle Felder gegangen ist, dann sagt die Spielleitung, wie viele Schätze auf der Route waren. Der Schatzsucher geht zurück zu seiner Gruppe und ein anderer Schatzsucher beginnt seinen Weg durch das Tal. Das Ziel des Spiels ist es, das die Schatzsuchergruppe genau auf Goldbarts Route geht und alle 5 Schätze hebt.
Dazu müssen die Schatzsucher in der Gruppe gut zusammenarbeiten und ihre jeweiligen Stärken finden. Einige von ihnen müssen sich bereits gegangene Wege merken und nachdenken welche neuen Wege die Gruppe ausprobieren soll. Einige müssen mehr graben für die Gruppe.
-
Eine Schülerin und ein Schüler spielen Goldbarts Schatztal
 Aufgabenstellung
Aufgabenstellung
Für das Spiel Goldbarts Schatztal muss sich der Spieleleiter Goldbarts Route durch das Tal überlegen. Kannst du ein Programm schreiben, damit dein micro:bit sich sofort einen zufälligen Weg durch das Tal überlegt, damit keine Pause zwischen den Spielen sein muss?
 Materialien
Materialien
• Micro:bit, USB-Kabel, Batterie • Computer • Abdeckklebeband
 Zeitaufwand
Zeitaufwand
1,5 Stunden
eine Stunde programmieren
eine halbe Stunde ausprobieren
 Schwierigkeitsgrad
Schwierigkeitsgrad
 Kompetenzen
Kompetenzen
Das solltest du bereits können:
Bewegung und Sport:
Entwickeln von Regelbewusstsein als Fähigkeit, Spielvereinbarungen und Spielregeln anzuerkennen, situativ abzuändern und neu zu gestalten Leisten und Wettkämpfen unter den Aspekten Leistungswille, Fairness und Umgang mit Sieg und Niederlage; Leistungsgrenzen erfahren und respektieren, aber auch durch eigenständiges Lernen und Üben verschieben.
Digitale Grundbildung:
erstellen einfache Programme oder Webanwendungen mit geeigneten Tools, um ein bestimmtes Problem zu lösen oder eine bestimmte Aufgabe zu erfüllen, kennen unterschiedliche Programmiersprachen und Produktionsabläufe.
 Unterrichtsfächer
Unterrichtsfächer
Bewegung und Sport Digitale Grundbildung
 Tipps und Hilfestellungen
Tipps und Hilfestellungen
Der micro:bit soll einen zufälligen Weg durch das 5x5 LED Raster anzeigen
Erforderliche Programmierblöcke
1. Variable

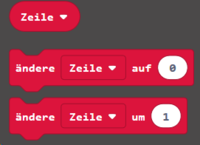
2. Wenn-Abfrage
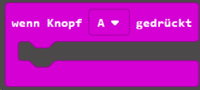
3. Zeige LEDs

4. Für-Schleife
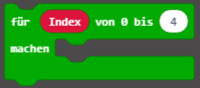
5. Wähle eine zufällige Zahl zwischen

6. Schalte eine LED ein
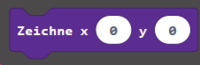
7. Beschränke eine Zahl/Variable

Eckpfeiler zur Programmierung
- Nachdem der Weg berechnet wurde, soll dieser beständig angezeigt werden, bis ein neuer Weg berechnet werden soll. Deswegen muss das Programm mit einem Tastendruck gestartet werden.
- Um jeden Punkt per Zufall zu bestimmen, benötigt man 2 Variablen, eine für die Spalte, in der man sich gerade befindet und eine für die Zeile.
- Der Weg soll von links nach rechts auf dem micro:bit verlaufen. Daher muss in jeder Spalte genau eine LED leuchten.
- Damit der Weg zu gehen ist, muss er durchgehend verlaufen. Das heißt zwischen den leuchtenden LEDs darf kein Abstand sein.
- Also kann in der nächsten Spalte immer nur die LED die eins höher, eins niedriger oder in derselben Höhe ist leuchten.
Schritt für Schritt zur Lösung
- Hinweise zur Lösungsfindung und auch eine mögliche, komplette Lösung findest du auf der Lösungsseite zu diesem Beispiel.
 Präsentation und Reflexion
Präsentation und Reflexion
- Stelle dein Ergebnis vor! Was kann dein Projekt?
- Was hat dir bei der Entwicklung deines Produkts gefallen?
- Welche Schwierigkeiten hattest du? Wie konntest du diese lösen?
- Erläutere, wie du dein Produkt programmiert hast! (Fachkompetenz stärken)
- Was war bei dieser Aufgabe interessant für dich?
 Weiterentwicklung
Weiterentwicklung
Was kannst du mit deiner Wegbestimmung sonst noch machen.
- 2 micro:bits gemeinsam stellen einen Weg über ein 10x5 Raster dar
- Vereinfachung: nur ein zufälliges Feld pro Spalte programmieren, statt einem zusammenhängenden Pfad
- Es sollen auch Pfade möglich sein, die nach unten, nach oben oder zurück gehen.
- Baue einen Zähler ein, der mit der Taste B die gefundenen Schätze mitzählt und mit Schütteln diese 2 Sekunden lang anzeigt.
- Mit dem vorliegenden Lösungsprogramm ist es ein wenig wahrscheinlicher, wenn die LED in der vorigen Spalte am Rand leuchtet, dass auch die LED in der nächsten Spalte am Rand leuchtet. Kannst du das Programm umschreiben, so dass es gleich wahrscheinlich ist, dass die LED am Rand oder ein Feld weiter drinnen leuchtet?
Dabei lernst du:
• Wie micro:bits miteinander kommunizieren
• Wie sich Wahrscheinlichkeiten auf Programme auswirken